yoncho`s blog
OpenCV 이미지 변환[1]_이미지 확대, 축소, 크기 조절, 대칭, 회전 | 특징 검출과 데이터 해석을 위한 이미지 전처리 본문
OpenCV 이미지 변환[1]_이미지 확대, 축소, 크기 조절, 대칭, 회전 | 특징 검출과 데이터 해석을 위한 이미지 전처리
욘초 2024. 9. 28. 14:33OpenCV에서 이미지 변환, 이미지 전처리 작업
이미지 변형이랑은 살짝 다른 변환은, 이미지 데이터 개수를 늘리거나 줄여서
연산량을 줄이는 것을 목표로 한다.
변환은 수학적으로 접근하면 (x, y)좌표값을 (x’, y’)값으로 변환하는 것을 의미한다.
OpenCV에서 변환은 크게 이미지의 크기 변환, 특정 요소의 위치 변경, 이미지의 회전 등이 있다.
유형으로는 강체 변환, 유사 변환, 선형 변환, 아핀 변환, 원근 변환이 있다.
- 강체 변환 : 평행이동과 회전 하는변환
- 유사 변환 : 평행이동과 회전, 크기조절 하는 변환
- 선형 변환 : 크기조절, 반사, 기울임 하는 변환
- 아핀 변환 : 크기조절, 반사, 기울임, 이동 하는 변환 (사각형을 평행사변형으로 바꾸는게 아핀 변환)
- 원근 변환 : 아핀변환과 유사하지만, 수평성은 유지되지않는다. (직선의 성질만 유지하고, 임의의 사각형으로 변한다.)
1. 확대 & 축소
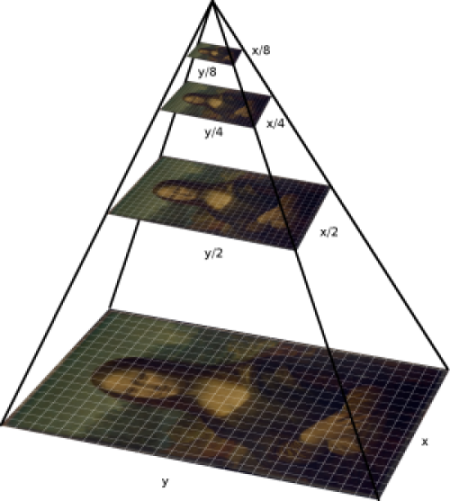
입력 이미지는 크기가 다 다르다, 그러나 알고리즘에서 요구하는 이미지의 크기는 어느정도 정해져있는 상황이다.
그러면 우리는 입력이미지의 크기를 줄여주거나 늘려줘야한다.
이미지 확대와 축소는 이미지 피라미드(image pyramid)를 활용해 단계별로 이미지를 샘플링한다.

- 업샘플링(up sampling) : 원본 이미지에서 크기를 확대하는 것, 하위 단계 이미지 생성
- 다운샘플링(down sampling) : 원본 이미지에서 크기를 축소하는 것, 상위 단계 이미지 생성
이미지 피라미드는 가우시안 피라미드 , 라플라시안 피라미드를 활용한다.
가우시안 피라미드
하위단계의 이미지를 생성하는 업샘플링과
상위단계의 이미지를 생성하는 다운샘플링을 사용한다.
업샘플링은 입력 이미지에 새로운 행과 열을 추가해서 짝수행과 짝수열로 만든 후 하위단계 이미지를 만든다.
즉, 입력 이미지가 M x N 사이즈라면 하위단계로 생성된 이미지의 크기는 2M x 2N이다.
다운샘플리은 반대로 입력 이미지의 짝수행과 짝수열을 제거해서 상위단계 이미지를 만든다.
즉, 입력 이미지가 M x N 사이즈라면 상위단계로 생성된 이미지의 크기는 M/2 x N/2이다.
면적으로 따지면 업샘플링은 4배, 다운샘플리은 1/4배로 이미지가 변형된 것이다.
잘 보면, 업샘플링은 입력 이미지에 새로운 행과 열 즉, 새로운 데이터를 추가하는 것이고
다운샘플링은 입력 이미지에 있던 기존 데이터에서 짝수행과 짝수열을 제거하는 것이므로,,
이미지를 업샘플링했다가 다운샘플링을 했다고 가정하면, 원본이미지와 결과이미지의 정보 데이터가 일치하지 않는다.
이럴 경우를 대비해,, 다운샘플링시 제거된 정보를 갖고와서 본래의 이미지로 복원해야된다.
라플라시안 피라미드
G(0) = Image
G(i + 1) = Down(G(i))
L(i) = G(i) - Up(G(i + 1))
G(0)은 입력 이미지를 의미하며, G(i)는 i번째 가우시안 피라미드 이미지를 의미한다.
G(i + 1)이미지를 만들기 위해 다운샘플링을 수행한다.
L(i)는 가우시안 피라미드로 만든 G(i)에서 업샘플링된 G(i + 1)을 감산해
가우시안 피라미드 레이어 간의 차이를 구한다.
이미지확대 (업샘플링) 함수
dst = cv2.pyrUp(
src,
dstSize = None,
borderType = None
)
- src : 입력이미지
- dstSize : 출력이미지의 크기, None이면 업샘플링을 한번 한다. 대부분 None으로 입력한다.
- borderType : 테두리 외삽법, 대부분 None으로 입력한다.
이미지 확대 함수는 입력 이미지에 새로운 행과 열을 추가한 뒤 0값으로 할당해준다.
이후 새로운 값을 할당하기위해서 근사값으로 채워 넣은 후, 가우시안 필터로 컨벌루션을 진행한다.
여기서 가우시안 필터는 4의 값을 갖고 정규화한다.
이미지축소 (다운샘플링) 함수
dst = cv2.pyrDown(
src,
dstSize = None,
borderType = None
)
- src : 입력이미지
- dstSize : 출력이미지의 크기, None이면 다운샘플링을 한번 한다. 대부분 None으로 입력한다.
- borderType : 테두리 외삽법, 대부분 None으로 입력한다.
이미지 축소 함수는 이미지에 흐림 효과를 적용한 후 다운 샘플링을 진행한다.
이미지 축소 함수 예제
import cv2
src = cv2.imread("bear.jpg")
dst = src.copy()
for i in range(3):
dst = cv2.pyrDown(dst)
cv2.imshow("dst", dst)
cv2.waitKey(0)
cv2.destroyAllWindows()2. 이미지 크기 조절
이미지 크기를 변형하는 것은 단순한 연산이 아니다. 이미지 확대를 할 경우, 픽셀에 대한 보간법을
이미지 축소를 할 경우, 픽셀에 대한 병합법을 사용한다.
이미지 크기 조절 함수는 사용자가 원하는 크기로 이미지를 변환한다.
조절 방법으로는 절대크기(임의의 크기)와 상대적크기(가로 ,세로 비율 맞게)
로 변경하는 방법이 있다.
이미지 크기 조절 함수
dst = cv2.resize(
src,
dsize,
fx = None,
fy = None,
interpolation = None
)
- src : 입력 이미지
- dszie : 절대 크기 필수 매개변수
- fx , fy : 상대 크기로, 상대크기로 할 경우 절대 크기를 (0, 0)으로 설정하고 fx, fy에 값을 넣어줘야 적용된다.
- interpolation : 보간법, 이미지의 비율을 변경하면 존재하지 않는 영역에 새로운 픽셀값을 매핑해야될 때가 있는데. 존재하는 가장 가까운 값들을 이용해 새로운 픽셀값을 얼마로 매핑해야되는지 결정하는 방법이다.
보간법
cv2.INTER_NEAREST : 가장 가까운 이웃 보간법 cv2.INTER_AREA : 영역 보간법 cv2.INTER_CUBIC : 4x4 큐빅 보간법
보간법이란??

값을 알고있는 두 지점 사이의 임의의 x좌표에 대해 y값을 추정하는 방법이다.
위 그림은 정확히 선형 보간법(linear interpolation)을 표현한 그림인데.
OpenCV에서 보간법은 두 픽셀 사이의 임의의 좌표 혹은 정수좌표가 아닌 실수좌표에대한 픽셀값을 얻을때 사용한다고 보면 된다.
이미지를 줄이거나 늘릴때 새롭게 할당해야되는 픽셀들은 대부분 분수 픽셀(실수 좌표)에 위치해있다. 이때 보간법에 따라 어떻게 매핑할지가 결정된다.
이웃 보간법 : 분수 픽셀 위치에서 제일 가까운 원본 픽셀을 결과이미지의 픽셀값으로 사용한다.
쌍 선형 보간법 : 분수 픽셀 위치에서 2x2 크기의 주변 원본 픽셀과 가까운 거리에 따라 선형적으로 가중치를 할당해서 결과 픽셀값으로 사용한다.
바이큐빅 보간법 : 분수 픽셀 위치에서 4x4크기의 주변 원본 픽셀을 3차원 큐빅 스플라인으로 계산해서 사용한다.
영역 보간법 : 픽셀 간의 관계를 고려해 리샘플링한다. 결과 이미지 픽셀위치를 입력 이미지 픽셀의 위치에 배치하고 겹치는 영역의 평균을 구해 결과 이미지의 픽셀값으로 사용한다.
기본적으로 쌍 선형 보간법을 가장 많이 활용하며,
이미지를 확대할 경우 쌍 선형 보간법이나 바이큐빅 보간법
이미지를 축소할 경우 영역 보간법을 주로 활용한다.
이미지 크기 조절 예제
import cv2
src = cv2.imread("car.png")
dst = src[280:310, 240:405]
dst = cv2.resize(dst, dsize = (256, 256), interpolation = cv2.INTER_NEAREST)
cv2.imshow("dst", dst)
cv2.waitKey(0)
cv2.destroyAllWindows()
3. 대칭 & 회전
대칭은 반사의 의미를 갖고있다.
변환할 행렬(이미지)에 2x2 행렬을 왼쪽 곱셈한다.
여기서 2x2행렬은 [[1, 0], [0, -1]] 또는 [[-1, 0], [0, 1]]이다.
정확히는 3x3행렬이지만 수평선은 유지되므로, 제외해서 2x2행렬로 쓰인다.
회전은 좌표값을 회전시키는 좌표 회전행렬과 좌표축을 회전시키는 좌표축 행렬이있다. 회전 행렬은 모두 원점(0, 0)을 기준으로 진행하며,
좌표 회전행렬은 원점을 기준으로 좌표값을 회전시켜 매핑한다.
좌표축 회전행렬은 원점을 기준으로 행렬 자체를 회전시켜 새로운 행렬값을 구성한다.
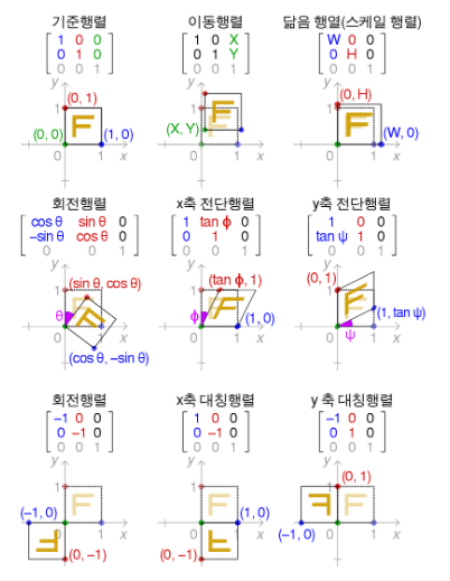
위 이미지에 대칭과 행렬에 대한 그림이 나와있다.
대칭 함수
dst = cv2.filp(
src,
flipCode
)
- src : 입력이미지
- flipCode : 대칭 축 플래그
대칭 축 플래그
- flipCode < 0 : XY축 대칭 (상하좌우)
- flipCode = 0 : X축 대칭 (상하 대칭)
- flipCode > 0 : Y축 대칭 (좌우 대칭)
회전 행렬은 원점을 중심으로 한 회전만 가능해서,, 임의의 중심점을 두고 회전하는 아핀 변환에 기반을 둔 회전을 해야한다.
그래서 2x3 아핀 변환 행렬을 사용해 임의의 중심을 기준으로 회전할 수 있다.

회전 행렬 생성 함수
dst = cv2.getRotationMatrix2D(
center,
angle,
scale
)
- center : 회전의 기준이 될 중심, 원점을 기준으로 회전하므로 (0, 0)이다.
- angle : 회전할 회전각도
- scale : 회전 후, 이미지의 확대 또는 축소 비율이다.
dst에는 2x3 매핑 변환 행렬(matrix)가 반환된다.
회전 행렬의 재할당 예제
import cv2
import math
src = cv2.imread("bear.jpg")
height, width, _ = src.shape
center = (width/2, height/2)
angle = 90
scale = 0.5
matrix = cv2.getRotationMatrix2D(center, angle, scale)
radians = math.radians(angle)
sin = math.sin(radians)
cos = math.cos(radians)
bound_w = int((height * scale * abs(sin)) + (width * scale * abs(cos)))
bound_h = int((height * scale * abs(cos)) + (width * scale * abs(sin)))
matrix[0, 2] += ((bound_w / 2) - center[0])
matrix[1, 2] += ((bound_h / 2) - center[1])
dst = cv2.warpAffine(src, matrix, (bound_w, bound_h))
cv2.imshow("dst", dst)
cv2.waitKey(0)
cv2.destroyAllWindows()
위 코드, 회전후 이미지 중심점이 중요코드이다.
'기술, 나의 공부를 공유합니다. > [ML] Object Detection' 카테고리의 다른 글
| OpenCV 이미지 검출[1]_가장자리 검출, 윤곽선 검출 | 주요 특징점 검출, 이미지내의 객체를 검출한다 (1) | 2024.09.28 |
|---|---|
| OpenCV 이미지 변환[2]_기하학적 변환, 모폴로지 변환 및 연산 | 특징 검출과 데이터 해석을 위한 이미지 전처리 (0) | 2024.09.28 |
| OpenCV 이미지 변형 | 특징 검출과 데이터 해석을 위한 이미지 전처리 (0) | 2024.09.28 |
| OpenCV 동영상 I/O | 동영상 입력 & 출력 (0) | 2024.09.28 |
| OpenCV 이미지 I/O | 이미지 입력 & 출력 (0) | 2024.09.28 |




